1.INTRODUCTION
Solid state is a state of matter besides liquid and gaseous state. In case of solids the inter molecular forces are very strong and empty spaces between the atoms/ions/ molecules is very less. That is why they have a fixed shape and volume.
1.1 Characteristic Properties of Solids Solids are characterised by the following properties * High density * Lowcompressibility * Rigidity * Definite shape and volume.
2. Classification of Solids
Solids are broadly classified on the basis of following parameters. * based on various properties * based on bonding present in building blocks.
2.1 On the basis of various properties Based on their various properties solids can be classified as * Crystalline solids * Amorphous solids.
Crystalline solids have a regular structure over the entire volume and sharp properties whereas amorphous solids have irregular structure over long distances and properties are not that sharp. Various differences are listed in table below.
| Crystalline Solids | Amorphous Solids |
| They have long range order | They have short range order. |
| They have definite melting point | They do not have definite melting point. |
| They have a definite heat of fusion | They do not have definite heat of fusion |
| They are rigid and incompressible | These may be compressed to some extent |
| They are given cleavage i.e. they break into two pieces with plane surfaces | They give irregular cleavage i.e. they break into two pieces with irregular surface |
| They are anisotropic | They are isotropic |
| There is a sudden change in volume when they melt. | There is no sudden change in volume on melting. |
| They possess symmetry | They do not possess any symmetry. |
| They possess interfacial angles. | They do not possess interfacial angles. |
2.2 Based on bonding
There are various type of solids based on type of bonding present in their building blocks. Various types of solids along with their properties are given in the table below.
3. STRUCTURE OF CRYSTALLINE SOLIDS
3.1 Crystal lattice and Unit Cell
The regular array of the building blocks (atoms/ions/molecules) inside the crystalline solid is called “Crystal Lattice”.
The smallest part or crystal lattice which can be repeated in all directions to generate entire crystal lattice is called “Unit Cell”. In unit cell the atoms of ions or molecules are represented by small spheres. Various lattices are formed by variation in following parameters :
* The edge length along 3 axes : a, b,c
* The interfacial angles : $ \alpha , \ \beta, \ \gamma $
* Location of atom/ions w.r.t each other in crystal lattice

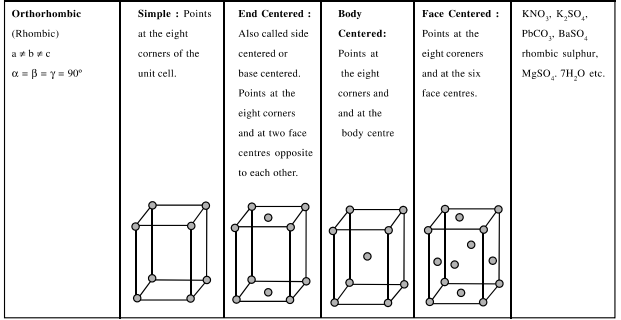
In all, there are seven types of unit cells and there can be some sub types of unit cells. These seven unit cells are called Primitive Unit Cells or Crystal Habits. Which are listed in table below lattice.
* Corners
* Body Centre
* Face Centres
Following are the contributions of a sphere kept at various locations.

* Location of spheres inside the unit cell.
* Rank of the unit cell (effective number of spheres inside a unit cell)
* Relation between edge length and radius of one sphere.
* Packing fraction (fraction of volume occupied by spheres in a unit cell)
The following parameters for all the 3 unit cells are listed is
the table below :
3.4 Density of cubic crystals
Density of cubic crystal is given by the following formula

Suppose we have spheres of equal size and we have to arrange them in a single layer with the condition that spheres should come in close contact with each other. Two types of layers are possible :
1. Square Packing
2. Hexagonal Packing
In square packing spheres are placed in such a way that the rows have a horizontal as well as vertical arrangement. In this case Co-ordination Number is 4.

2. On other hand if spheres of second layer are placed in depressions of first layer we get BCC unit cell and ABAB ..... type of packing. Arrangements based on hexagonal foundation layer are as follows :
If we put 2nd layer in depressions of first hexagonal layer A two types of voids are created. X type of voids are those which are hollow and through voids of layerA and layer B. While Y type of voids are those voids of layer B which are exactly above spheres of layer A. If we place the spheres of 2nd layer on Y voids then we are repeating layer 1 and ABABAB.... type packing is obtained. In this arrangement hexagonal unit cell is obtained and packing is called Hexagonal Close Packing (HCP). The efficiency of this packing is 74%.
If the 3rd layer is placed on X-type of voids then a new layer C is obtained and then the arrangement will berepeated. We will obtain ABCABCABC..... type of packing. The unit cell for this arrangement is FCC and the packing effeciency is 74%.
Radius ratio $=\frac{r}{R}$
It forms by contact of 4 spheres and is positioned at the centre of tetrahedron formed by contact of 4 spheres.
4.3.4 Cubic Void
Key Points:

6.2 Vacancies
These are defects that occur when positions that should contain atoms or ions are vacant.
Sometimes atoms or ions may occupy these positions.
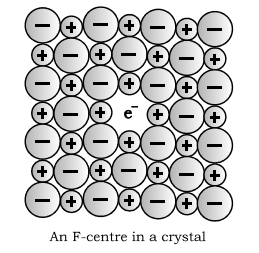
Due to anionic vacancies : The anion may be missing from its lattice site leaving an e” behind so that charge remains balanced. The site containing electron is called F centre. They import colour to the crystal, F stands for Farbenzenter meaning colour. This defect is similar to schottky defect and is found is crystals having schottky defect eq. NaCl, KCl etc.
























No comments:
Post a Comment